Dijkstra's algorithm

In our daily lives, most of us are travelling frequently from Point A to Point B, now this might be your home to your office or to your mistress who nobody knows about, you need a tool that navigates you through your ethically ambiguous journey. There is no better tool than GPS on our phones which we can rely on to take us toward our destination. Now the joke was that the GPS tools were taking us through some bizarre paths and they were somewhat unreliable, this was in the early smartphone era where map data around the world was scarce and the algorithms that created these paths were not very much optimized. Today, thanks to advanced imaging and large quantities of mapping data this problem has become a thing of the past. The algorithm which almost every Computer Science student has learned or at least heard of had published back in 1956 by Dutch computer scientist Dr. Edsger W.Dijkstra

Brief introduction of graph concepts

To explain Dijkstra's algorithm, one should need to understand the basic concepts of graphs. In short, graphs are data structures that are used to denote connections between pairs of elements. We call these elements nodes. Sometimes these nodes are directed, which means for example we can go from A to B but not from B to A. As a final concept, there is the weight property which denotes the weight of a certain connection, this can be thought of as the distance between points.

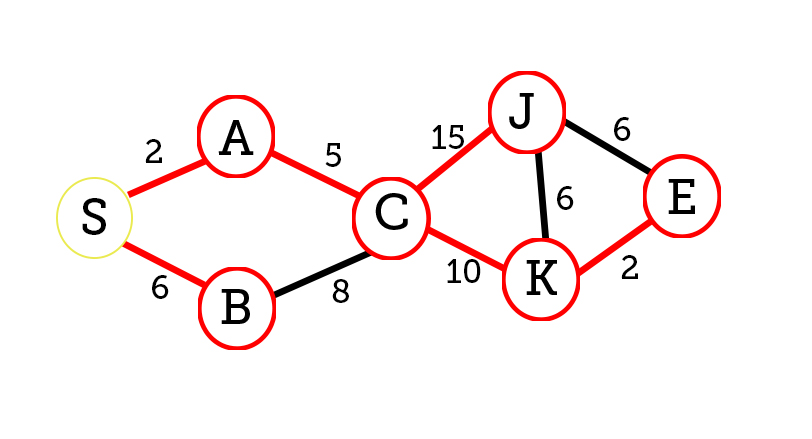
The algorithm starts at the chosen node and keeps track of the currently known shortest distance from each of the connections to the starting node and it updates when it finds a shorter path. Once it found the shortest connection that node is marked as visited and added to the path. This goes on until all the nodes have been added to the path. To demonstrate I put together an example graph to further understand the concepts.

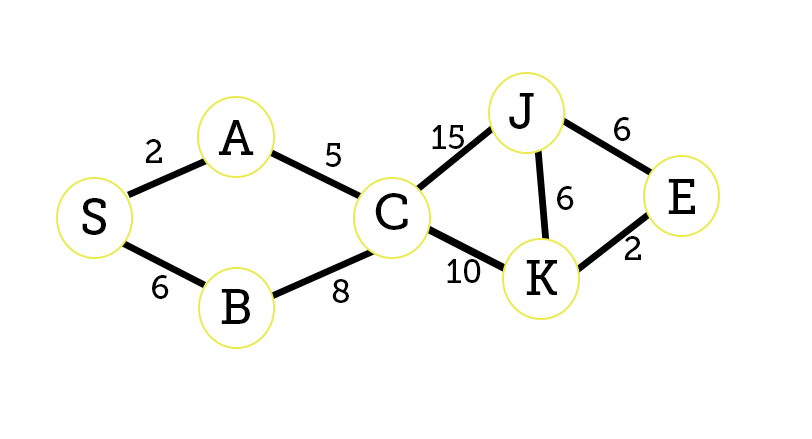
We will keep track on what is the shortest path from node S (start) to E (end) and also list the shortest path to every individual node.

Distance: S=0, A=∞, B=∞, C=∞, J=∞, K=∞, E=∞

Unvisited nodes:{A, B, C, J, K, E}

At this point, we need to check the distance from starting node to the neighboring nodes.After that, we need to update the distance list

Distance: S=0, A=2, B=6, C=∞, J=∞, K=∞, E=∞

Then we need to select the node that is closest to the starting node and mark it as visited and also add it to our path.

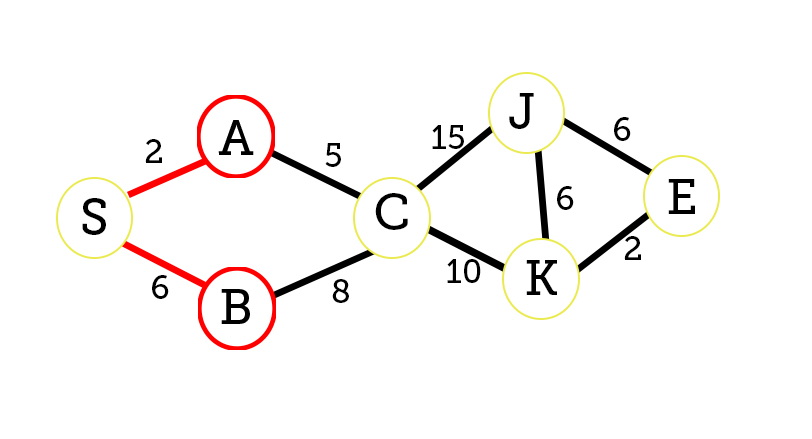
Unvisited nodes:{B, C, J, K, E}

At this point, we need to further analyze the new adjacent nodes and update our distance list. Since we already analyzed node B, we only need to update the new node C.

Distance: S=0, A=2, B=6, C=7, J=∞, K=∞, E=∞

Before going through the other junction, we will backtrack and analyze the node B to C

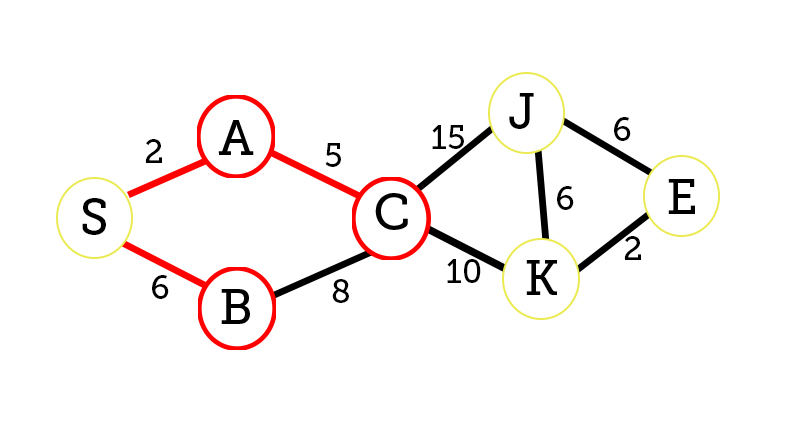
C = 2+5 vs 6+8 shortest is 2+5=7

Distance: S=0, A=2, B=6, C=7, J=∞, K=∞, E=∞

Unvisited nodes:{J, K, E}

We continue updating our node distances

J= 2+5+15 K=2+5+10

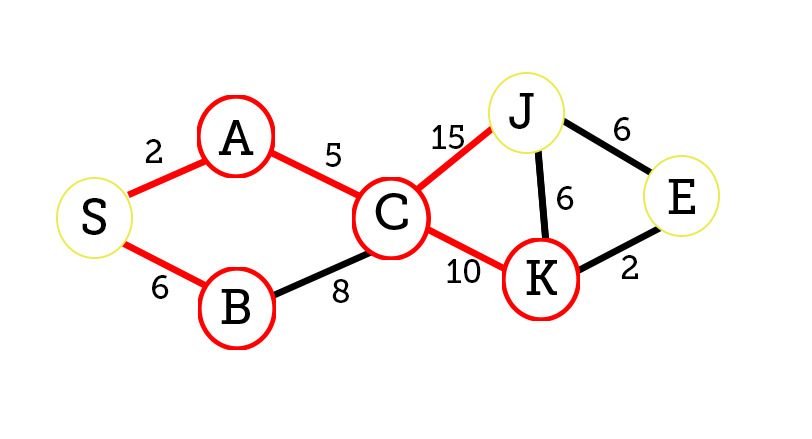
Unvisited nodes:{J, E}

We will continue through the K junction to find the node E

node E= 2+5+10+2 vs 2+5+15+6 =19

node E becomes 19 and therefore the shortest path from S to E becomes:
S => A =>C => K =>E

Conclusion

To summarize all that we have talked about, Dijkstra's algorithm helps us find the shortest path in a given graph. It is used on navigation systems, although a modified version of some sort, because in this algorithm we check every possible node to reach our final destination, let's say we want to apply a large graph, then it becomes inefficient to check for all nodes. This algorithm is highly optimized later on to give priorities to certain nodes in order to be more efficient and faster.

Source section

• Abbas, S. H. (n.d.). What is Dijkstra's algorithm? Educative. Retrieved April 11, 2023, from https://www.educative.io/answers/what-is-dijkstras-algorithm
• Dodsworth, D. (2023, March 14). Dijkstra's shortest path algorithm explained, with examples. History. Retrieved April 11, 2023, from https://history-computer.com/dijkstras-shortest-path-algorithm-explained-with-examples/
• Navone, E. C. (2022, February 3). Dijkstra's shortest path algorithm - a detailed and visual introduction. freeCodeCamp.org. Retrieved April 11, 2023, from https://www.freecodecamp.org/news/dijkstras-shortest-path-algorithm-visual-introduction/